1793.타일링
(*)이번문제는 백준에 있는 1793번 타일링이다.
dp에 속하는 메모이제이션을 공부하기 좋은 문제이며 long long int보다 커서 출력이 어려울 때
구현하는 Big interger도 활용할 수 있는 문제이다.
이해하는데 좀 많은 시간이 걸린 것 같다. 재귀함수가 특히 나는 너무 헷갈린다..쩝.. 그래도 이해했으니 성공!
1793번: 타일링
문제 2×n 직사각형을 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×17 직사각형을 채운 한가지 예이다. 입력 입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있으며, 숫자 0 ≤ n ≤ 250이 주어진다. 출력 입력으로 주어지는 각각의 n마다, 2×n 직사각형을 채우는 방법의 수를 출력한다. 예제 입력 1 복사 2 8 12 100 200 예제 출력 1 복사 3 171
www.acmicpc.net
< Code 설명 >
#include <iostream>
#include <algorithm>
using namespace std;
string d[251];
string big(string a, string b){
int sum=0;
string result;
while( sum || !a.empty() || !b.empty()){
if(!a.empty()){
sum += a.back()-'0'; // 문자를 숫자로 바꿔주기위해 '0'을 빼줌
a.pop_back(); // sum에 넣어서 연산했기 때문에 제거
}
if(!b.empty()){
sum += 2*(b.back()-'0'); // 문자를 숫자로 바꿔주기위해 '0'을 빼줌
// 2*(n-2)이므로 2를 곱해줌
b.pop_back(); // sum에 넣어서 연산했기 때문에 제거
}
result.push_back((sum%10)+'0'); // 올림하거나 남은 나머지를 다시 문자로
// result에 저장
sum/=10; // 올림된 값을 저장
}
reverse(result.begin(),result.end()); // 뒤집어서 계산했기 때문에 마지막에 뒤집는다.
return result;
}
string dp(int n){
if(n==1 || n==0) // 2x1 경우나 타일을 추가하지 않는 경우
return "1"; // 1개이므로 '1'리턴
// n=0 인경우를 빼먹으면 안됨
if(n==2) // 2x2인 경우
return "3"; // 3개의 경우의 수가 있으므로 '3' return
if(d[n]!="")
return d[n];
return d[n]=big(dp(n-1),dp(n-2)); 점화식을 big interger로 계산
}
int main()
{
int n;
while(cin >> n){
cout << dp(n) << endl;
}
return 0;
}
반드시 알아야 할 TIP!!
# 이번 문제에서 알아야할 것은 바로 DP 문제를 풀 때 정확한 점화식을 세워야 한다는 것이다.
# 또하나 중요한점이 있다면 점화식을 세우고나서도 반복되는 점화식이 있다면 2차원 DP를 활용하는 센스가 필요하다!
우선 점화식을 구해야하는데 점화식을 구하려면 상황을 제시해보면 된다.
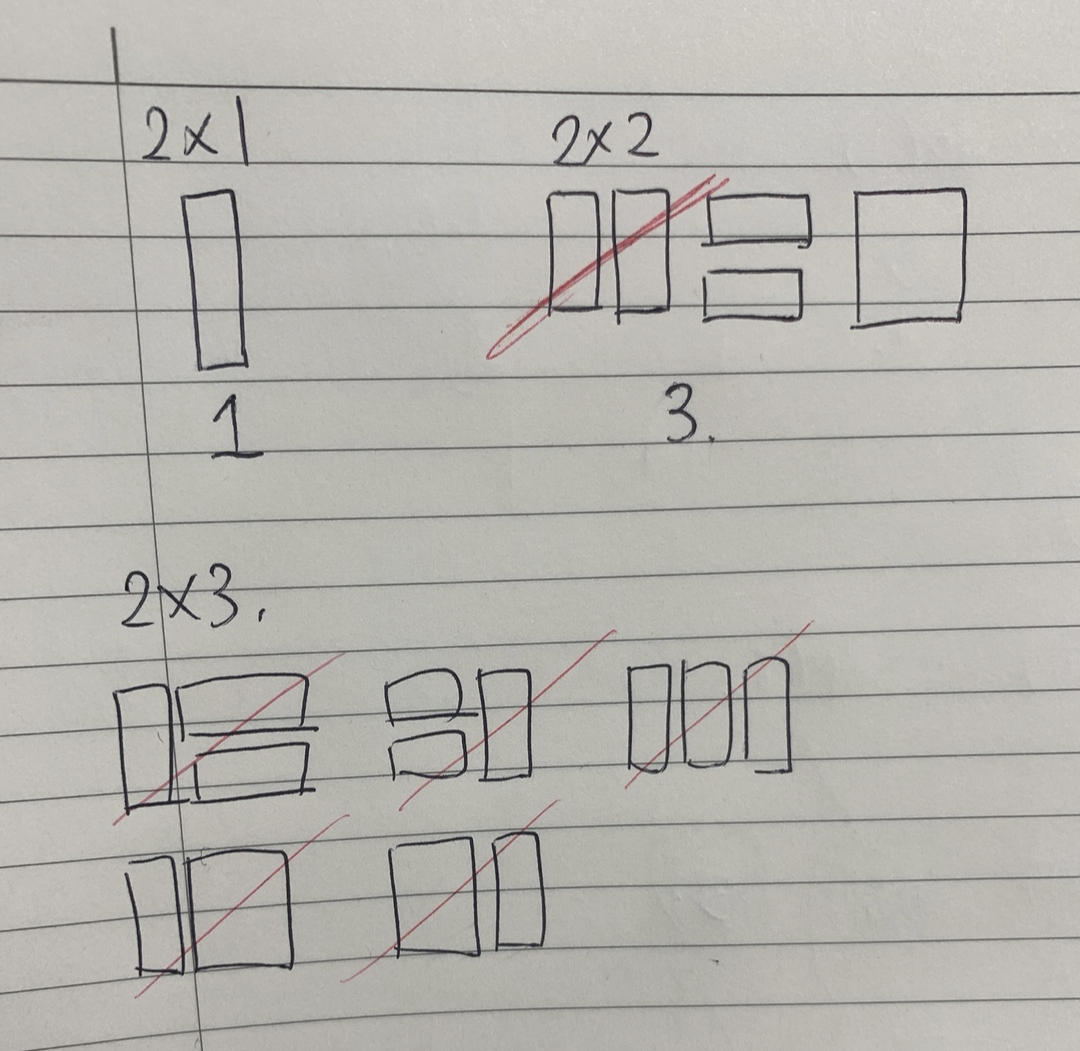
2x1의 타일이 올 경우는 1개
2x2의 타일이 올 경우는 3개
2x3의 타일이 올 경우는 5개이다.
여기서 규칙성을 발견하는 것이 점화식을 만들어낼 때 가장 중요하다.
하지만 자세히 살펴보면 2x2로 구성할 수 있는 타일에 형태에는 2x1의 형태에 포함되는 것들이 있다.
그렇기 때문에 2가지로 봐야한다. 2x3의 경우는 보다시피 2x1이나 2x2의 형태에 모두 포함되어 있기 때문에
점화식에 들어갈 수 없다. 그 이후의 타일의 형태도 마찬가지이다. 그러므로 점화식을 작성해보면

그림과 같은 형태가 되기 때문에 d[n]=dp(n-1) + 2*d(n-2)가 된다. 하지만 이 문제에서는 크기가 long long int보다
길어지기 때문에 string으로 나타내어야한다. 이 때 이용되는 것이 Big Integer와 메모이제이션이고 우리가 필요한 내용들을
저장하고 존재한다면 굳이 연산을 하지 않고 가져다 쓰는 방식으로 중복 연산을 제거하는 방식이다.
Big integer 참조 : https://travelbeeee.tistory.com/193