-
1197.최소 스패닝 트리알고리즘/백준 BAEK JOON 2020. 8. 20. 22:40
이번에 풀어볼 문제는 백준 1197번 최소 스패닝 트리이다.
이전 포스팅에서 스패닝 트리를 공부했다면 이번에는 간선에 가중치가 들어있어서
최소한의 간선으로 연결하되, 가중치도 최소로 진행하는 최소 스패닝 트리 문제를 풀어보았다.
직접 구현하는 방법에 대해서 공부할 수 있는 문제이다. 이해가 안간다면 코드를 보거나 그림을 그려서 공부해보자
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 �
www.acmicpc.net
이 문제는 크루스칼 알고리즘과 프림 알고리즘으로 풀이할 수 있다.
크루스칼 알고리즘에서의 핵심 풀이는 바로 1차원배열을 이용하여 부모노드에 대한 정보를 저장하는 것이다.
부모노드는 간단하게 말해 해당 정점이 연결되는 시작의 역할을 하는 정점이라고 생각하면 된다.
=> 해당 정점이 연결된 바로 이전 노드라고 생각하면 안된다! => 직접 그림을 그리면서 진행하면 이해에 도움된다.
=> 쉽게 말하자면 간선 선택 "진행 중"에 정점과의 연결된 가장 시작점의 노드라고 표현하는 것이 좋을 것 같다.
=> "진행 중"의 정점의 부모노드 라는 것이 중요하다 모든 정점이 연결되고 나서의 부모 노드를 의미하는 것이 아니다.
< 예시 > 다음은 내가 만든 테스트 케이스다.
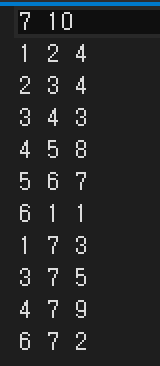
이런식이라면 그림은 다음과 같아진다.
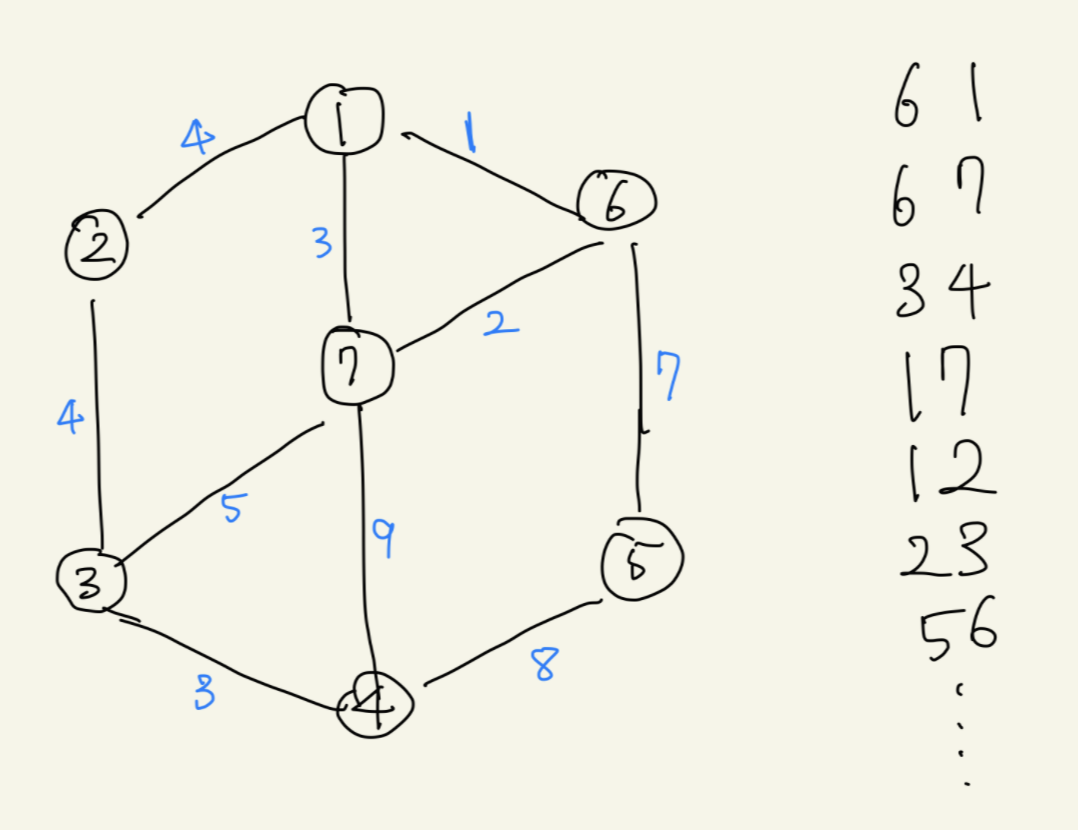
간선의 정보를 가중치로 오름차순 정렬하여 오른쪽에 적어두었다.

해당 간선의 정보대로 부모노드를 정해주며 알고리즘을 진행한 모습이다.
정점 1과 정점 7의 부모노드는 6이 되었다. 정점 4의 부모노드는 3이되었다.
그럼 이번에는 완성된 노드를 보자.

위에서 오해하지말라고 했던 것은 최소 스패닝 트리 완성 후, 부모노드를 체크하게 되면
알고리즘 "진행 중"에서의 부모노드와 다르게 보인다. 4의 부모노드는 3이 아니라 5가 된다.
그 이유는 설계한 내용대로 잘 흘러갔기 때문이다. 잘못되었다는 말이 아니라
최종적으로 판단할 때는 부모 노드들을 따라가야 최종 부모 노드가 나온다는 의미이다.
무슨말이냐하면 해당 그림에서 3의 부모노드는 6이고 6의 부모노드는 5로 저장될 것이다.
그러므로 최종 부모노드를 판단할 때는 4 -> 3 -> 6 -> 5 가 되어서 4의 부모노드는 5가 되는 것이다.
알고리즘 "진행 중"에서의 부모노드를 찾는 로직이 find( ) 함수에서의 27번 라인이다.
( 혹시나 그림을 그리면서 진행했는데 왜 4의 부모노드는 3이지?? 잘못한건가??로 끝나지 않길 바라며 적어보았다 )
< Code 설명 - 크루스칼 알고리즘 >
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475
#pragma warning(disable:4996)#include <iostream>#include <vector>#include <algorithm>#define MAX 10001using namespace std;int node[MAX]; // 알고리즘 진행 중에서의 부모노드가 저장되는 배열int V, E, ans; // 정점, 간선, 정답struct line{ // 간선 정보int x, y, len; // a, b, 가중치bool operator<(line const &a){ // 내부 연산자 오버로딩return len < a.len; // => 이렇게 해야 가중치를 sort로 오름차순 정렬이 가능함}};vector<line> v; // 간선 정보가 저장되는 vectorint find(int x){if (node[x] == x) // 노드 idx번호와 노드값이 같으면 아직 부모노드가 없다는 의미이므로return x; // 연결을 위해 그대로 리턴else // 근데 부모노드가 있다면return node[x] = find(node[x]); // 해당 노드의 부모노드 값을 재귀를 통해 찾아서 리턴}void merge(int x, int y){ // 두 정점을 연결함x = find(x); // 첫 번째 정점의 부모 노드값y = find(y); // 두 번째 정점의 부모 노드값if (x!=y) // 두 부모노드의 값이 다르다면node[y] = x; // 두 번째 정점의 부모노드를 정해줌}bool check_node(int x, int y){ // 부모노드가 같은지 다른지 판단x = find(x); // 정점의 부모노드 확인y = find(y); // 정점의 부모노드 확인if (x == y) // 같으면 부모노드가 같다는 의미로 => 서로 연결되어 있다는 의미이기 때문에 사이클이 형성될 수도 있음return false; // 그러므로 거짓 리턴elsereturn true; // 부모노드가 다르면 연결}void kru(){for (int i = 0; i < E; i++){ // 간선의 숫자 만큼 확인if (check_node(v[i].x, v[i].y)){ // 두 정점이 같은 부모노드를 가지는지 확인// 서로 다른 부모를 가진 정점이라면 => 연결이 안되어있다는 의미merge(v[i].x, v[i].y); // 서로 다른 정점을 연결ans += v[i].len; // 해당 가중치의 간선을 연결함(우리는 최소 가중치를 구해야하므로 누산)}}}int main() {freopen("1197.txt", "r", stdin);cin >> V >> E;int a, b, c;for (int i = 0; i < E; i++){cin >> a >> b >> c;v.push_back({ a, b, c }); // 간선의 정보 저장}sort(v.begin(), v.end()); // 가중치 순으로 오름차순 정렬for (int i = 1; i <= V; i++) // 부모 노드 체크를 위한 배열node[i] = i; // 간선이 연결되지 않았다고 생각하고 시작되기 때문에 초기 값을 자기자신이 된다.kru(); // 크루스칼 진행cout << ans << endl;return 0;}cs 반응형'알고리즘 > 백준 BAEK JOON' 카테고리의 다른 글
19236.청소년상어 (0) 2020.09.09 19238.스타트 택시 (0) 2020.08.30 9372.상근이의 여행 (0) 2020.08.20 1932.정수 삼각형 (0) 2020.08.19 1074.Z (0) 2020.08.15 댓글